Arus bolak-balik satu fasa

Memperoleh arus bolak-balik

Jika kawat A diputar dalam fluks magnet yang dibentuk oleh dua kutub magnet searah jarum jam (Gbr. 1), maka ketika kawat melintasi garis medan magnet, itu akan menginduksi e. d. s yang nilainya ditentukan oleh ekspresi

E = Bvsinα,

di mana B adalah induksi magnetik dalam T, l adalah panjang kawat dalam m, v adalah kecepatan kawat dalam m / s, α — sudut di mana kawat memotong garis medan magnet.

Misalkan B, I dan v untuk kasus ini tetap konstan, maka induksi e. dll. c. hanya akan bergantung pada sudut α di mana kawat melintasi medan magnet. Jadi, pada titik 1, ketika kawat bergerak di sepanjang garis medan magnet, nilai ggl induksi. dll. p akan menjadi nol ketika kawat bergerak ke titik 3 oe. dll. v. akan menjadi yang paling penting, karena garis gaya akan dilintasi oleh konduktor dalam arah tegak lurus terhadapnya, dan akhirnya, mis. dll. v. akan mencapai nol lagi jika kawat dipindahkan ke titik 5.

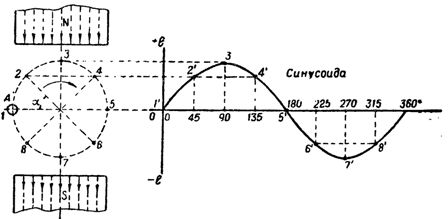
Beras. 1. Mengubah induksi e. dll. pp. dalam kawat berputar dalam medan magnet

Pada titik tengah 2 dan 4, di mana kawat melintasi garis gaya pada sudut α = 45 °, nilai ggl induksi. dll. c akan secara bersamaan kurang dari pada titik 3. Jadi, ketika kawat diputar dari titik 1 ke titik 5, yaitu sebesar 180 °, induksi e. dll. v. perubahan dari nol ke maksimum dan kembali ke nol.

Cukup jelas bahwa pada putaran lebih lanjut kawat A melalui sudut 180 ° (melalui titik 6, 7, 8 dan 1), sifat perubahan induksi e. dll. p. akan sama, tetapi arahnya akan berubah menjadi sebaliknya, karena kawat akan melintasi garis medan magnet yang sudah berada di bawah kutub lain, yang setara dengan melintasinya ke arah pertama yang berlawanan.

Oleh karena itu, ketika kawat diputar 360 °, induksi e. dll. v. tidak hanya berubah besarnya sepanjang waktu, tetapi juga mengubah arahnya dua kali.

Jika kabel ditutup ke beberapa resistansi maka kabel akan muncul listrik, juga bervariasi dalam ukuran dan arah.

Arus listrik, yang besarnya dan arahnya terus berubah, disebut arus bolak-balik.

Apa itu gelombang sinus?

Sifat perubahan e. dll. (arus) untuk satu putaran kabel untuk kejelasan yang lebih besar, mereka secara grafis direpresentasikan menggunakan kurva. Karena nilai e. dll. c sebanding dengan sinα, kemudian, setelah menetapkan sudut tertentu, dengan bantuan tabel, dimungkinkan untuk menentukan nilai sinus dari setiap sudut, dan pada skala yang sesuai untuk membuat kurva untuk perubahan e. dll. c.Untuk melakukan ini, pada sumbu horizontal kita akan menyisihkan sudut rotasi kawat, dan pada sumbu vertikal, dalam skala yang sesuai, e. dll. dengan

Jika sebelumnya ditunjukkan pada gambar.1 hubungkan titik-titik tersebut dengan garis lengkung yang halus, maka akan memberikan gambaran besarnya dan sifat perubahan induksi e. dll. (arus) pada setiap posisi konduktor dalam medan magnet. Karena kenyataan bahwa nilai induksi e. dll. p. setiap saat ditentukan oleh sinus sudut di mana kawat melintasi medan magnet yang ditunjukkan pada gambar. 1 kurva disebut sinusoidal, dan e. dll. s.- sinusoidal.

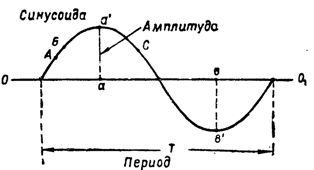
Beras. 2. Sinusoid dan nilai karakteristiknya

Perubahan yang kami lihat e. dll. c secara sinusoidal sesuai dengan rotasi kawat dalam medan magnet pada sudut 360 °. Ketika kawat diputar 360 ° berikutnya, perubahan induksi e. dll. s.(dan arus) akan muncul lagi dalam gelombang sinus, yaitu akan berulang secara berkala.

Dengan demikian, disebabkan oleh e. dll. c disebut arus listrik sinusoidal arus bolak-balik... Cukup jelas bahwa tegangan yang dapat kita ukur di ujung kabel A, dengan adanya rangkaian eksternal tertutup, juga akan berubah secara sinusoidal.

Arus bolak-balik yang diperoleh dengan memutar kawat dalam fluks magnet atau sistem kabel yang terhubung dalam koil disebut arus bolak-balik fase tunggal.

Arus bolak-balik sinusoidal adalah yang paling banyak digunakan dalam teknologi. Namun, Anda dapat menemukan arus bolak-balik yang tidak berubah menurut hukum sinus. Arus bolak-balik seperti itu disebut non-sinusoidal.

Lihat juga: Apa itu arus bolak-balik dan apa bedanya dengan arus searah

Amplitudo, periode, frekuensi arus bolak-balik fase tunggal

Kekuatan saat ini, berubah sepanjang sinusoid, berubah terus menerus. Jadi, jika di titik A (Gbr. 2) arusnya sama dengan 3a, maka di titik B sudah lebih besar.Di beberapa titik lain di sinusoid, misalnya di titik C, arus sekarang akan memiliki nilai baru, dan seterusnya.

Kekuatan arus pada waktu tertentu ketika berubah sepanjang sinusoid disebut nilai arus sesaat.

Nilai sesaat terbesar dari arus bolak-balik fase tunggal disebut ketika itu berubah sepanjang amplitudo sinusoidal... Sangat mudah untuk melihat bahwa untuk satu putaran kawat, arus mencapai nilai amplitudonya dua kali. Salah satu nilai aa 'positif dan ditarik dari sumbu 001 dan bv lainnya negatif dan ditarik ke bawah dari sumbu.

Waktu selama diinduksi e. dll. (atau gaya saat ini) melewati seluruh siklus perubahan, yang disebut siklus bulanan T (Gbr. 2). Periode biasanya diukur dalam detik.

Kebalikan dari periode disebut frekuensi (f). Dengan kata lain, frekuensi arus bolak-balik adalah jumlah periode per satuan waktu, yaitu dalam hitungan detik. Jadi, misalnya, jika arus bolak-balik dalam 1 detik mengasumsikan nilai dan arah yang sama sepuluh kali lipat, maka frekuensi arus bolak-balik tersebut adalah 10 periode per detik.

Untuk mengukur frekuensi, alih-alih jumlah periode per detik, satuan yang disebut hertz (hertz) digunakan. Frekuensi 1 hertz sama dengan frekuensi 1 lps / detik. Saat mengukur frekuensi tinggi, akan lebih mudah menggunakan unit 1000 kali lebih besar daripada hertz, mis. kilohertz (kHz), atau 1.000.000 kali lebih besar dari hertz — megahertz (mhz).

Arus bolak-balik yang digunakan dalam teknologi, tergantung pada frekuensinya, dapat dibagi menjadi arus frekuensi rendah dan arus frekuensi tinggi.

Nilai rms AC

Arus searah yang melewati kawat memanaskannya. Jika Anda menjalankan arus bolak-balik melalui kabel, kabel juga akan memanas.Hal ini dapat dimaklumi, karena meskipun arus bolak-balik berubah arah sepanjang waktu, pelepasan panas sama sekali tidak bergantung pada arah arus pada kawat.

Ketika arus bolak-balik dilewatkan melalui bola lampu, filamennya akan menyala. Pada frekuensi arus bolak-balik standar 50 Hz, tidak akan ada kedipan cahaya, karena filamen bola lampu pijar, yang memiliki inersia termal, tidak memiliki waktu untuk mendingin pada saat arus dalam rangkaian nol. Penggunaan arus bolak-balik dengan frekuensi kurang dari 50 Hz untuk penerangan sekarang tidak diinginkan karena fakta bahwa fluktuasi intensitas bohlam yang tidak menyenangkan dan melelahkan mata muncul.

Melanjutkan analogi arus searah, kita dapat berharap bahwa arus bolak-balik yang mengalir melalui kawat tercipta di sekitarnya Medan gaya. Sebenarnya arus bolak-balik tidak menimbulkan medan magnet, tetapi karena medan magnet yang ditimbulkannya juga akan berubah arah dan besarnya.

Arus bolak-balik berubah sepanjang waktu baik dalam besaran maupun arahNS. Secara alami, muncul pertanyaan tentang bagaimana mengukur variabel T dengan baik, dan berapa nilainya ketika berubah sepanjang sinusoid harus diambil sebagai penyebab tindakan ini atau itu.

C Untuk tujuan ini, arus bolak-balik dibandingkan dalam hal aksi yang dihasilkannya dengan arus searah, yang nilainya tetap tidak berubah selama percobaan.

Misalkan arus searah mengalir melalui kawat dengan resistansi konstan 10 A dan diketahui bahwa kawat tersebut dipanaskan hingga suhu 50 °.Jika sekarang kita melewati kabel yang sama bukan arus searah, tetapi arus bolak-balik, jadi kita memilih nilainya (bertindak, misalnya, dengan rheostat) sehingga kabel juga dipanaskan hingga suhu 50 °, lalu masuk dalam hal ini kita dapat mengatakan bahwa aksi arus bolak-balik sama dengan aksi arus searah.

Memanaskan kabel dalam kedua kasus ke suhu yang sama menunjukkan bahwa dalam satuan waktu arus bolak-balik mengeluarkan jumlah panas yang sama dengan arus searah pada kabel.

Arus sinusoidal bolak-balik yang memancarkan resistansi tertentu per satuan waktu jumlah panas yang sama dengan arus searah yang setara besarnya dengan arus searah... Nilai arus ini disebut nilai efektif (Id) atau nilai efektif dari arus bolak-balik .. Oleh karena itu, untuk contoh kita, nilai efektif arus bolak-balik adalah 10 A... Dalam hal ini, nilai arus maksimum (puncak) akan melebihi nilai rata-rata besarnya.

Pengalaman dan perhitungan menunjukkan bahwa nilai efektif arus bolak-balik lebih kecil dari nilai amplitudonya dalam √2 (1,41) kali. Oleh karena itu, jika nilai puncak arus diketahui, maka nilai efektif arus Id dapat ditentukan dengan membagi amplitudo arus Ia dengan √2, yaitu Id = Aza/√2

Sebaliknya jika nilai rms arus diketahui maka dapat dihitung nilai puncak arus yaitu Ia = Azd√2

Hubungan yang sama berlaku untuk amplitudo dan nilai rms dari e. dll. v. dan voltase: Satuan = Ea /√2, Ud = Uа/√2

Alat pengukur paling sering menunjukkan nilai aktual, oleh karena itu, ketika notasi, indeks «d» biasanya dihilangkan, tetapi Anda tidak boleh melupakannya.

Impedansi di sirkuit AC

Ketika konsumen induktansi dan kapasitansi dihubungkan ke sirkuit AC, aktif dan reaktansi harus dipertimbangkan (reaktansi terjadi ketika kapasitor menyala atau tersedak di sirkuit AC). Oleh karena itu, ketika menentukan arus yang melewati konsumen seperti itu, tegangan suplai harus dibagi dengan impedansi rangkaian (konsumen).

Impedansi (Z) rangkaian AC satu fasa ditentukan dengan rumus berikut:

Z = √(R2 + (ωL — 1 / ωC)2

di mana R adalah resistansi aktif rangkaian dalam ohm, L adalah induktansi rangkaian dalam henries, C adalah kapasitansi rangkaian (kapasitor) dalam farad, ω — frekuensi sudut arus bolak-balik.

Konsumen yang berbeda digunakan dalam rangkaian arus bolak-balik di mana perlu untuk mempertimbangkan tiga nilai R, L, C atau hanya beberapa di antaranya. Pada saat yang sama, frekuensi sudut arus bolak-balik harus diperhitungkan.

Untuk beberapa pengguna, hanya nilai R dan L yang dapat diperhitungkan pada nilai frekuensi sudut yang sesuai, misalnya pada frekuensi AC 50 Hz kumparan solenoida atau belitan generator hanya dapat dianggap mengandung resistansi aktif dan induktif. Dengan kata lain, kapasitansi dalam hal ini dapat diabaikan. Kemudian impedansi AC dari pengguna tersebut dapat dihitung dengan rumus:

Z = √(R2 + ω2L2)

Jika koil atau koil yang dirancang untuk operasi arus bolak-balik dihubungkan ke arus searah dengan tegangan yang sama, arus yang sangat besar akan mengalir melalui koil, yang dapat menyebabkan pembangkitan panas yang signifikan, dan insulasi koil dapat rusak. Sebaliknya , arus kecil akan mengalir melalui kumparan yang dirancang untuk beroperasi dalam rangkaian arus searah dan terhubung ke rangkaian arus bolak-balik dengan tegangan yang sama, dan perangkat yang menggunakan kumparan ini tidak akan melakukan tindakan yang diperlukan.

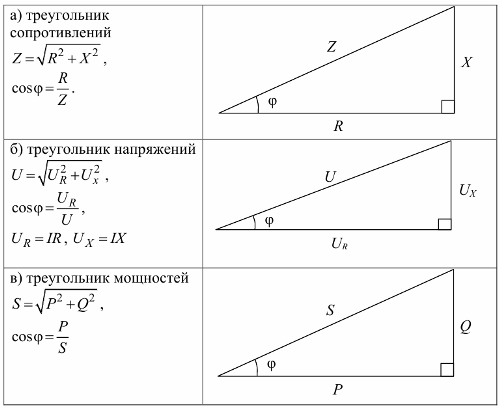
Segitiga resistansi, segitiga tegangan, dan segitiga daya: