Apa itu pasokan listrik?

Manusia modern selalu menjumpai listrik dalam kehidupan sehari-hari dan di tempat kerja, menggunakan perangkat yang mengkonsumsi arus listrik dan perangkat yang menghasilkannya. Saat bekerja dengan mereka, Anda harus selalu mempertimbangkan kemampuan mereka yang melekat pada karakteristik teknis.

Salah satu indikator utama perangkat listrik apa pun adalah kuantitas fisik energi listrik... Biasanya disebut intensitas atau kecepatan pembangkitan, transmisi atau konversi listrik menjadi jenis energi lain, misalnya panas, cahaya, mekanis.

Pengangkutan atau pemindahan energi listrik yang besar untuk keperluan industri dilakukan menurut saluran listrik tegangan tinggi.

Transformasi energi listrik dilakukan di gardu transformator.

Konsumsi listrik terjadi pada perangkat rumah tangga dan industri untuk berbagai keperluan. Salah satu tipe umum mereka adalah lampu pijar dari berbagai peringkat.

Daya listrik generator, saluran listrik, dan konsumen di sirkuit DC dan AC memiliki arti fisik yang sama, yang secara bersamaan dinyatakan dalam rasio yang berbeda tergantung pada bentuk sinyal komposit. Untuk menentukan pola umum, pengertian nilai sesaat... Mereka kembali menekankan ketergantungan laju transformasi listrik pada waktu.

Penentuan daya listrik sesaat

Dalam teknik kelistrikan teoretis, untuk mendapatkan hubungan dasar antara arus, tegangan, dan daya, gambar mereka dalam bentuk nilai sesaat, yang ditetapkan pada titik waktu tertentu, digunakan.

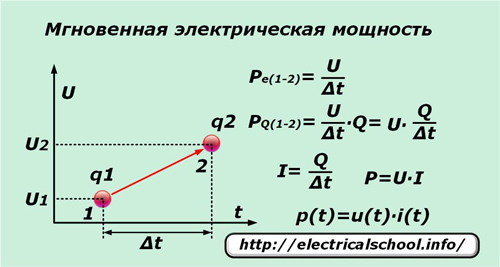
Jika dalam waktu yang sangat singkat ∆t satu muatan dasar q di bawah pengaruh tegangan U bergerak dari titik «1» ke titik «2», maka ia melakukan pekerjaan yang sama dengan beda potensial antara titik-titik ini. Membaginya dengan selang waktu ∆t, kita mendapatkan persamaan daya sesaat per satuan muatan Pe (1-2).

Karena tidak hanya muatan tunggal yang bergerak di bawah aksi tegangan yang diberikan, tetapi juga semua muatan yang berdekatan yang berada di bawah pengaruh gaya ini, yang jumlahnya mudah diwakili oleh angka Q, nilai sesaat dari daya PQ (1-2) dapat ditulis untuk mereka.

Setelah melakukan transformasi sederhana, kami memperoleh ekspresi untuk daya P dan ketergantungan nilai sesaatnya p (t) pada komponen hasil kali arus sesaat i (t) dan tegangan u (t).

Penentuan daya listrik konstan

V sirkuit DC besarnya penurunan tegangan pada bagian rangkaian dan arus yang mengalir melaluinya tidak berubah dan tetap stabil, sama dengan nilai sesaat.Oleh karena itu, daya dalam rangkaian ini dapat ditentukan dengan mengalikan nilai-nilai ini atau membagi pekerjaan sempurna A dengan periode pelaksanaannya, seperti yang ditunjukkan pada gambar penjelasan.

Penentuan daya listrik arus bolak-balik

Hukum variasi arus dan tegangan sinusoidal yang ditransmisikan melalui jaringan listrik memaksakan pengaruhnya pada ekspresi daya di sirkuit semacam itu. Daya semu berperan di sini, yang dijelaskan oleh segitiga daya dan terdiri dari komponen aktif dan reaktif.

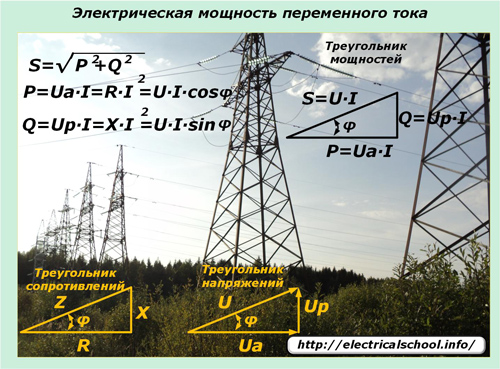
Arus listrik sinusoidal ketika melewati saluran listrik dengan jenis beban campuran di semua bagian tidak mengubah bentuk harmoniknya, dan penurunan tegangan pada beban reaktif bergeser dalam fase ke arah tertentu. Ekspresi nilai momen membantu untuk memahami pengaruh beban yang diterapkan pada perubahan daya di sirkuit dan arahnya.

Pada saat yang sama, segera perhatikan fakta bahwa arah aliran arus dari generator ke konsumen dan daya yang ditransmisikan melalui rangkaian yang dibuat adalah hal yang sama sekali berbeda, yang dalam beberapa kasus mungkin tidak hanya bertepatan, tetapi juga diarahkan berlawanan arah.

Pertimbangkan hubungan ini dalam perwujudan ideal dan murni untuk berbagai jenis muatan:

• aktif;

• kapasitif;

• induktif.

Disipasi daya beban aktif

Kita akan berasumsi bahwa generator menghasilkan tegangan sinusoidal ideal u yang diterapkan pada resistansi aktif murni dari rangkaian. Ammeter A dan voltmeter V mengukur arus I dan tegangan U setiap waktu t.

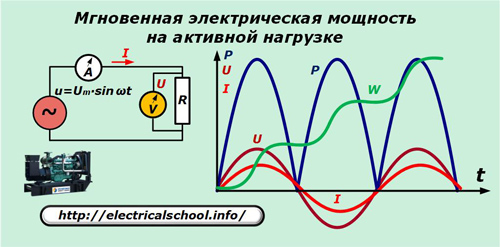
Grafik menunjukkan bahwa sinusoid arus dan penurunan tegangan melintasi resistansi aktif cocok dalam frekuensi dan fase, membuat osilasi yang sama. Gaya yang diekspresikan oleh produk mereka berosilasi pada frekuensi dua kali lipat dan selalu tetap positif.

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt).

Jika kita pergi ke ekspresi tegangan operasi, maka kita dapatkan: p = P ∙ (1-cos2ωt).

Kami kemudian akan mengintegrasikan daya selama periode satu osilasi T dan kami akan dapat melihat bahwa perolehan energi ∆W selama interval ini meningkat. Seiring waktu, resistansi terus mengkonsumsi porsi listrik baru, seperti yang ditunjukkan pada grafik.

Dengan beban reaktif, karakteristik konsumsi energinya berbeda, bentuknya berbeda.

Disipasi daya kapasitif

Di sirkuit listrik generator, ganti elemen resistif dengan kapasitor kapasitansi C.

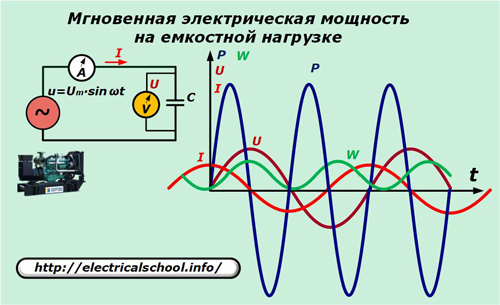
Hubungan antara penurunan arus dan tegangan dalam kapasitansi dinyatakan dengan rasio: I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

Kami mengalikan nilai ekspresi sesaat arus dengan tegangan dan mendapatkan nilai daya yang dikonsumsi oleh beban kapasitif.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ sin2ωt = U2/ (2X° C) ∙ sin2ωt.

Di sini Anda dapat melihat bahwa daya berfluktuasi sekitar nol pada dua kali frekuensi tegangan yang diberikan. Nilai totalnya untuk periode harmonik, serta perolehan energinya, adalah nol.

Ini berarti bahwa energi bergerak di sepanjang sirkuit tertutup dari sirkuit di kedua arah, tetapi tidak bekerja.Fakta seperti itu dijelaskan oleh fakta bahwa ketika tegangan sumber meningkat dalam nilai absolut, daya menjadi positif, dan aliran energi melalui rangkaian diarahkan ke wadah tempat energi terkumpul.

Setelah tegangan melewati bagian harmonik jatuh, energi dikembalikan dari kapasitor ke rangkaian ke sumber. Tidak ada pekerjaan berguna yang dilakukan dalam kedua proses tersebut.

Disipasi daya dalam beban induktif

Sekarang, di rangkaian suplai, ganti kapasitor dengan induktansi L.

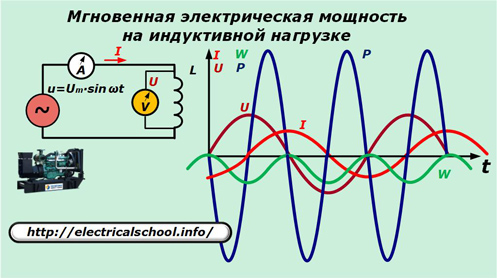
Di sini arus melalui induktansi dinyatakan dengan rasio:

I = 1 / L∫udt = -Um / ωL ∙ cos ωt.

Lalu kita dapatkan

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL) ∙ sin2ωt = -U2/ (2ХL) ∙ sin2ωt.

Ekspresi yang dihasilkan memungkinkan kita untuk melihat sifat perubahan arah daya dan peningkatan energi pada induktansi, yang melakukan osilasi yang sama yang tidak berguna untuk melakukan pekerjaan, seperti pada kapasitansi.

Daya yang dilepaskan dalam beban reaktif disebut komponen reaktif. Dalam kondisi ideal, ketika kabel penghubung tidak memiliki resistansi aktif, kabel tersebut tampak tidak berbahaya dan tidak menyebabkan kerusakan apa pun. Tetapi dalam kondisi daya nyata, transien periodik dan fluktuasi daya reaktif menyebabkan pemanasan semua elemen aktif, termasuk kabel penghubung, yang menghabiskan sebagian energi dan nilai daya penuh sumber yang diterapkan berkurang.

Perbedaan utama antara komponen daya reaktif adalah tidak melakukan pekerjaan yang bermanfaat sama sekali, tetapi menyebabkan hilangnya energi listrik dan beban berlebih pada peralatan, yang sangat berbahaya dalam situasi kritis.

Untuk alasan ini, untuk menghilangkan pengaruh daya reaktif, khususnya sistem teknis untuk kompensasinya.

Distribusi daya pada beban campuran

Sebagai contoh, kami menggunakan beban generator dengan karakteristik kapasitif aktif.

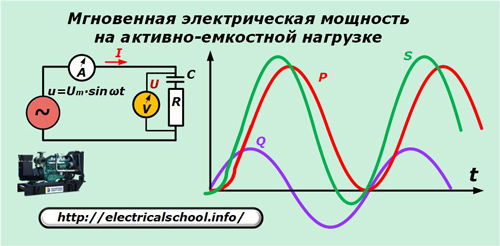
Untuk menyederhanakan gambar, sinusoidal arus dan tegangan tidak ditampilkan dalam grafik yang diberikan, tetapi harus diingat bahwa dengan sifat kapasitif aktif dari beban, vektor arus mendahului tegangan.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ).

Setelah transformasi kita mendapatkan: p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt.

Kedua istilah dalam ekspresi terakhir ini adalah komponen aktif dan reaktif dari daya semu sesaat. Hanya yang pertama yang berfungsi dengan baik.

Alat pengukur daya

Untuk menganalisis konsumsi listrik dan menghitungnya, digunakan alat pengukur yang sudah lama disebut «Penghitung»… Pekerjaan mereka didasarkan pada pengukuran nilai efektif arus dan tegangan dan secara otomatis mengalikannya dengan keluaran informasi.

Meter menampilkan konsumsi energi dengan menghitung waktu pengoperasian peralatan listrik secara bertahap dari saat meter dinyalakan di bawah beban.

Untuk mengukur komponen aktif daya di sirkuit AC, pengukur watt, dan reaktif - varmeters. Mereka memiliki sebutan unit yang berbeda:

• watt (W, W);

• var (var, var, var).

Untuk menentukan konsumsi energi total, perlu dihitung nilainya menggunakan rumus segitiga daya berdasarkan pembacaan wattmeter dan varmeter. Itu dinyatakan dalam unitnya sendiri - volt-ampere.

Penunjukan unit yang diterima dari masing-masing membantu teknisi listrik untuk menilai tidak hanya nilainya, tetapi juga sifat komponen daya.