Resonansi arus

Koneksi paralel kapasitor dan induktor dalam rangkaian arus bolak-balik

Pertimbangkan fenomena dalam rantai arus bolak-balikberisi generator, kapasitor dan induktor yang terhubung secara paralel. Asumsikan bahwa sirkuit tidak memiliki resistansi aktif.

Jelas, dalam rangkaian seperti itu tegangan koil dan kapasitor setiap saat sama dengan tegangan yang dihasilkan oleh generator.

Arus total dalam suatu rangkaian terdiri dari arus di cabang-cabangnya. Arus di cabang induktif tertinggal dari tegangan dalam fase seperempat periode, dan arus di cabang kapasitif memimpinnya dengan seperempat periode yang sama. Oleh karena itu, arus di cabang-cabang setiap saat berubah menjadi fase-bergeser relatif satu sama lain selama setengah periode, yaitu, mereka berada dalam antifase. Dengan demikian, arus di cabang setiap saat diarahkan satu sama lain, dan arus total di bagian sirkuit yang tidak bercabang sama dengan selisihnya.

Ini memberi kita hak untuk menulis persamaan I = IL -rangkaian integral

dimana saya- nilai efektif arus total dalam rangkaian, I L dan sirkuit terpadu — nilai efektif arus di cabang.

Menggunakan hukum Ohm untuk menentukan nilai efektif arus di cabang, kita mendapatkan:

Il = U / XL dan Az° C = U / XC

Jika rangkaian didominasi oleh resistansi induktif, yaitu. XL More ▼ XC, arus di koil lebih kecil dari arus di kapasitor; oleh karena itu arus di bagian rangkaian yang tidak bercabang bersifat kapasitif dan rangkaian secara keseluruhan untuk generator akan bersifat kapasitif. Sebaliknya, dengan XC lebih besar dari XL, arus di kapasitor lebih kecil dari arus di koil; oleh karena itu arus di bagian rangkaian yang tidak bercabang adalah induktif, dan rangkaian keseluruhan untuk generator akan menjadi induktif.

Tidak boleh dilupakan bahwa dalam kedua kasus bebannya reaktif, mis. sirkuit tidak mengkonsumsi daya generator.

Resonansi arus

Sekarang mari kita pertimbangkan kasus ketika kapasitor dan koil yang terhubung secara paralel ternyata sama dalam reaktansinya, yaitu. XlL = X°C.

Jika, seperti sebelumnya, kita mengasumsikan bahwa kumparan dan kapasitor tidak memiliki resistansi aktif, maka jika reaksinya sama (YL = Y° C), arus total di bagian rangkaian yang tidak bercabang akan menjadi nol, sedangkan di cabangnya sama. arus akan mengalir dengan besaran terbesar. Dalam hal ini, fenomena arus resonansi terjadi di sirkuit.

Pada resonansi arus, nilai efektif arus di setiap cabang, ditentukan oleh rasio IL = U / XL dan Аz° С = U / XC akan sama satu sama lain, sehingga XL = XC.

Kesimpulan yang kami capai mungkin tampak agak aneh pada pandangan pertama. Faktanya, generator dimuat dengan dua resistansi dan tidak ada arus di bagian sirkuit yang tidak bercabang, sementara arus yang sama dan, terlebih lagi, arus terbesar mengalir di resistansi itu sendiri.

Ini dijelaskan oleh perilaku medan magnet koil dan medan listrik kapasitor… Pada resonansi arus, seperti pada resonansi tegangan, ada fluktuasi energi antara bidang kumparan dan bidang kapasitor. Generator, setelah mengkomunikasikan energi ke sirkuit, tampak terisolasi. Ini dapat dimatikan sepenuhnya dan arus di bagian sirkuit yang bercabang akan dipertahankan tanpa generator oleh energi yang awalnya disimpan oleh sirkuit. Selain itu, tegangan di terminal sirkuit akan tetap sama persis dengan tegangan yang dihasilkan oleh generator.

Jadi, ketika induktor dan kapasitor dihubungkan secara paralel, kami memperoleh rangkaian osilator yang berbeda dari yang dijelaskan di atas hanya karena generator yang menghasilkan osilasi tidak terhubung langsung ke rangkaian dan rangkaian tertutup. 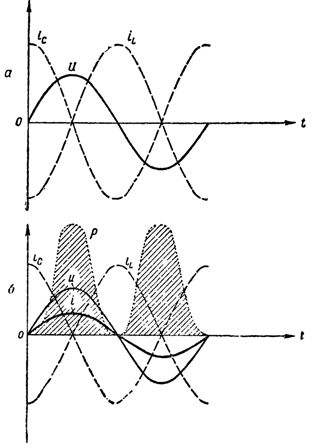Grafik arus, tegangan dan daya dalam rangkaian pada resonansi arus: a — resistansi aktif sama dengan nol, rangkaian tidak mengkonsumsi energi; b - sirkuit memiliki resistansi aktif, arus muncul di bagian sirkuit yang tidak bercabang, sirkuit mengkonsumsi energi

L, C dan e, di mana resonansi arus terjadi, ditentukan, seperti pada resonansi tegangan (jika kita mengabaikan resistansi aktif rangkaian), dengan persamaan:

ωL = 1 / ω° C

Karena itu:

eres = 1 / 2π√LC

Lres = 1 / ω2C

Sepotong = 1 / ω2L

Dengan mengubah salah satu dari ketiga besaran ini, persamaan Xl = X°C dapat dicapai, yaitu mengubah rangkaian menjadi rangkaian berosilasi.

Jadi, kami memiliki rangkaian osilasi tertutup di mana kami dapat menginduksi osilasi listrik, mis. arus bolak-balik. Dan jika bukan karena resistansi aktif yang dimiliki setiap sirkuit berosilasi, arus bolak-balik mungkin terus ada di dalamnya.Kehadiran resistansi aktif mengarah pada fakta bahwa osilasi di sirkuit secara bertahap mereda, dan untuk mempertahankannya, diperlukan sumber energi - alternator.

Di sirkuit arus non-sinusoidal, mode resonansi dimungkinkan untuk berbagai komponen harmonik.

Arus resonansi banyak digunakan dalam praktik. Fenomena resonansi arus digunakan dalam filter bandpass sebagai "penjepit" listrik yang menunda frekuensi tertentu. Karena ada resistansi arus yang signifikan pada frekuensi f, penurunan tegangan pada rangkaian pada frekuensi f akan maksimum. Properti loop ini disebut selektivitas, digunakan pada penerima radio untuk mengisolasi sinyal dari stasiun radio tertentu. Sirkuit berosilasi yang beroperasi dalam mode arus resonansi adalah salah satu komponen utama generator elektronik.