Sirkuit listrik dengan arus non-sinusoidal

Arus non-sinusoidal dan dekomposisinya

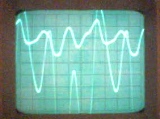Dalam rangkaian listrik, arus non-sinusoidal dapat terjadi karena dua alasan:

1. sirkuit listrik itu sendiri adalah linier, tetapi tegangan non-sinusoidal bekerja pada sirkuit,

2. tegangan yang bekerja pada rangkaian adalah sinusoidal, tetapi rangkaian listrik mengandung elemen non-linear.

Mungkin ada kedua alasan tersebut. Bab ini membahas sirkuit untuk poin pertama saja. Dalam hal ini, tegangan non-sinusoidal dianggap periodik.

Generator pulsa periodik digunakan di berbagai perangkat teknik radio, otomasi, telemekanik. Bentuk pulsa bisa berbeda: gergaji, berundak, persegi panjang (Gbr. 1).

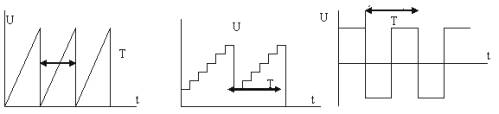
Gambar 1. Bentuk pulsa

Fenomena yang terjadi dalam rangkaian listrik linier di bawah tegangan periodik tetapi non-sinusoidal paling mudah dipelajari jika kurva tegangan diperluas dalam deret Fourier trigonometri:

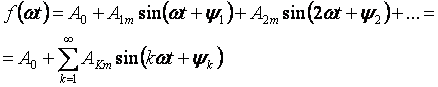
Suku pertama deret A0 disebut komponen konstanta atau harmonik nol, suku kedua deret tersebut

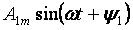
- harmonik fundamental atau pertama dan semua anggota lain dari bentuk

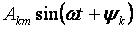
untuk k> 1 disebut harmonik yang lebih tinggi.

Jika pada ekspresi (3.1) kita membuka sinus dari penjumlahan, maka kita dapat berpindah ke bentuk penulisan deret lainnya:

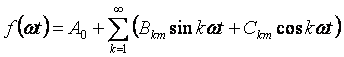Jika fungsinya simetris terhadap sumbu absis, maka deret tersebut tidak mengandung komponen konstanta. Jika fungsinya simetris terhadap sumbu ordinat, maka deret tersebut tidak mengandung sinus. Fungsinya simetris terhadap titik asal dan tidak mengandung kosinus.

Beberapa contoh ekspansi seri diberikan dalam tabel. 1 dan mereka juga tersedia dalam literatur referensi.

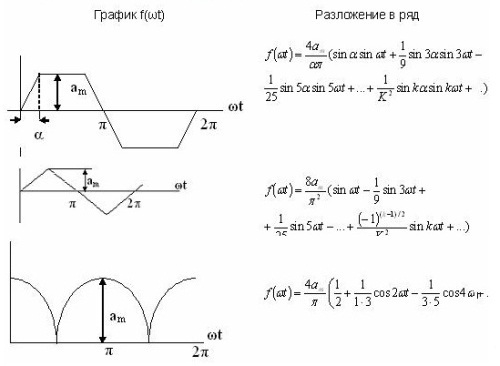
Tabel 1. Ekspansi deret Fourier

Perhitungan rangkaian arus non-sinusoidal

Rangkaian dihitung untuk setiap harmonik sesuai dengan modelnya. Rangkaian dihitung sebanyak harmonisa pada tegangan yang bekerja pada rangkaian. Dalam hal ini, perlu mempertimbangkan sejumlah karakteristik.

Perlu dicatat bahwa resistansi elemen induktif meningkat dengan meningkatnya bilangan harmonik

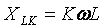
dan elemen kapasitif, sebaliknya, berkurang:

Juga harus diperhitungkan bahwa komponen arus konstan tidak melewati kapasitor dan induktansi bukanlah resistansi terhadapnya.

Selain itu, orang tidak boleh melupakan kemungkinan fenomena resonansi tidak hanya pada harmonik fundamental, tetapi juga pada harmonik yang lebih tinggi.

Diagram vektor dapat diplot untuk setiap harmonik secara terpisah.

Menurut prinsip superposisi, arus setiap cabang dapat terdiri dari jumlah suku individu (harmonik nol, fundamental, dan lebih tinggi):

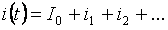
Nilai rms dari arus cabang total dapat ditentukan oleh nilai rata-rata arus harmonik individu:

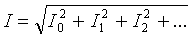
Daya aktif arus non-sinusoidal sama dengan jumlah daya aktif harmonik individu:

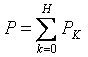
Di bawah ini adalah contoh umum untuk menghitung rangkaian arus non-sinusoidal. Semua arus, tegangan, resistansi akan memiliki dua indeks: digit pertama berarti nomor cabang dan digit kedua adalah nomor harmonik. Tegangan masukan:

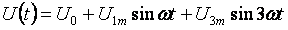
• Komponen permanen

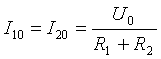
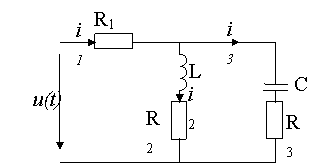
Gambar 2. Diagram kelistrikan

• Harmonik Utama:

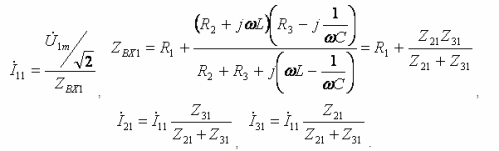
• harmonik ketiga:

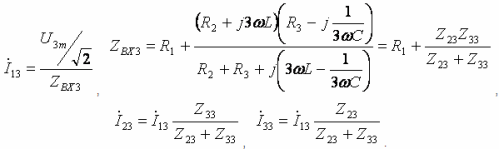
Baca juga: Skema perbaikan AC ke DC yang paling umum